Page personnelle d'Olivier Garet

Thèmes de recherche

Mon domaine de recherche principal est une branche des probabilités que l'on appelle la mécanique statistique.
L'idée générale est que l'on étudie des systèmes infinis de particules en essayant d'établir le lien entre les propriétés microscopiques (par exemple l'interaction entre des particules proches) et les propriétés macroscopiques (par exemples les caractéristiques à grande échelle des mesures d'équilibre.)

Systèmes infinis de particules
Percolation
Environnements aléatoires
Mesures de Gibbs sur un réseau
Dynamiques stochastiques gradients infini-dimensionnelles


#!/usr/local/bin/julia

## version du 19/02/2023

using LightGraphs;
using Plots;

function dessin(n,p)
 (NH,NV)=(n,n)
 origine=round(Int64,NH*(NV/2-1)+NH/2)
 # code du site au centre de la grille   
 g=SimpleGraph(NH*NV)
 # création du graphe
 for i=1:NH-1,j=1:NV
  point=NH*(j-1)+i
  # graphe: création des arêtes horizontales
  if (rand()<=p) add_edge!(g,point,point+1) end
  # graphe: création des arêtes verticales
  if (rand()<=p) add_edge!(g,point,point+NH) end  
 end
paths=dijkstra_shortest_paths(g,origine)
temps=reshape(paths.dists,(n,n))
return(temps)
end # dessin

(n,p)=(1000,0.55)
s=min.(dessin(n,p),n*2/3)
heatmap(s,ratio=1,size=(2*n,2*n))
savefig("distance_chimique-$p-$n.png")

Le dessin à gauche est une réalisation de l'ensemble des points du cluster infini pour la percolation de Bernoulli de paramètre 0.55 qui sont à une distance (en nombre d'aretes) inférieure ou égale a t=666 de l'origine. La couleur utilisée pour peindre un point est fonction de sa distance à l'origine.
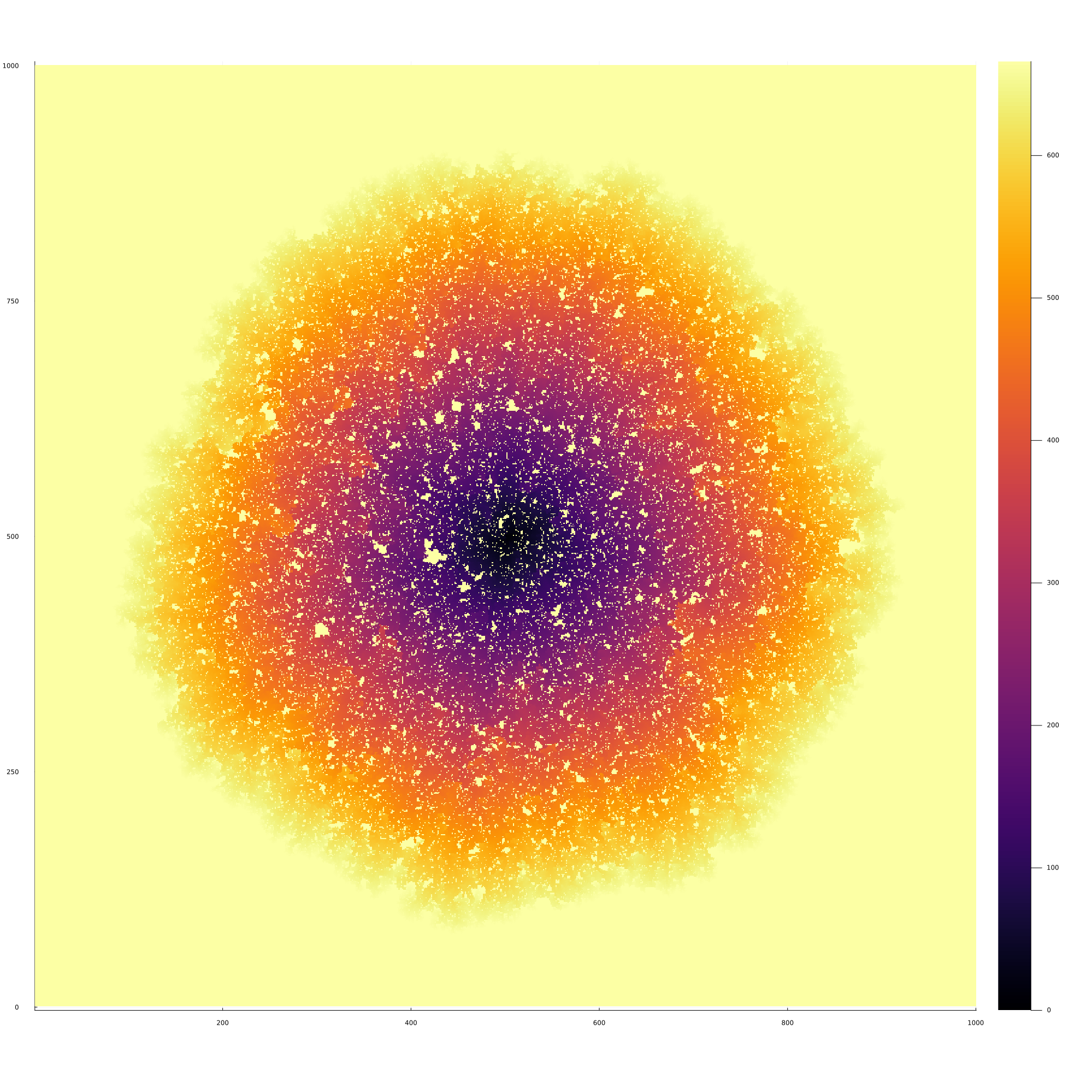
A droite, le code Julia pour générer l'image (clic droit, enregistrer ici pour télécharger).
Avec Régine Marchand , nous avons démontré que lorsque t tend vers l'infini, cet ensemble admet une forme asymptotique limite non aléatoire. (Voir cet article .)

D'autres images pour la distance chimique

Thèse de doctorat et HDR

Habilitation à diriger des recherches: Quelques problèmes de mécanique statistique.
Soutenue le 12 décembre 2005

mémoire au format postscript. mémoire au format pdf.

Thèse de doctorat: Mesures de Gibbs gaussiennes et dynamiques aléatoires associées sur $\R^{\Z^d}$.
Directrice de thèse: Sylvie Roelly
Soutenue le 19 novembre 1998

Résumé de ma thèse sur l'Annuaire des Thèses. ma thèse au format ps gzippé. ma thèse au format pdf.